CLEAVING¶
The LAMMPS package CLEAVING contains all the modified potentials and additional computes/fixes needed by the cleaving model to use Thermodynamic Integration to calculate the Surface Free Energy of a given system.
Background¶
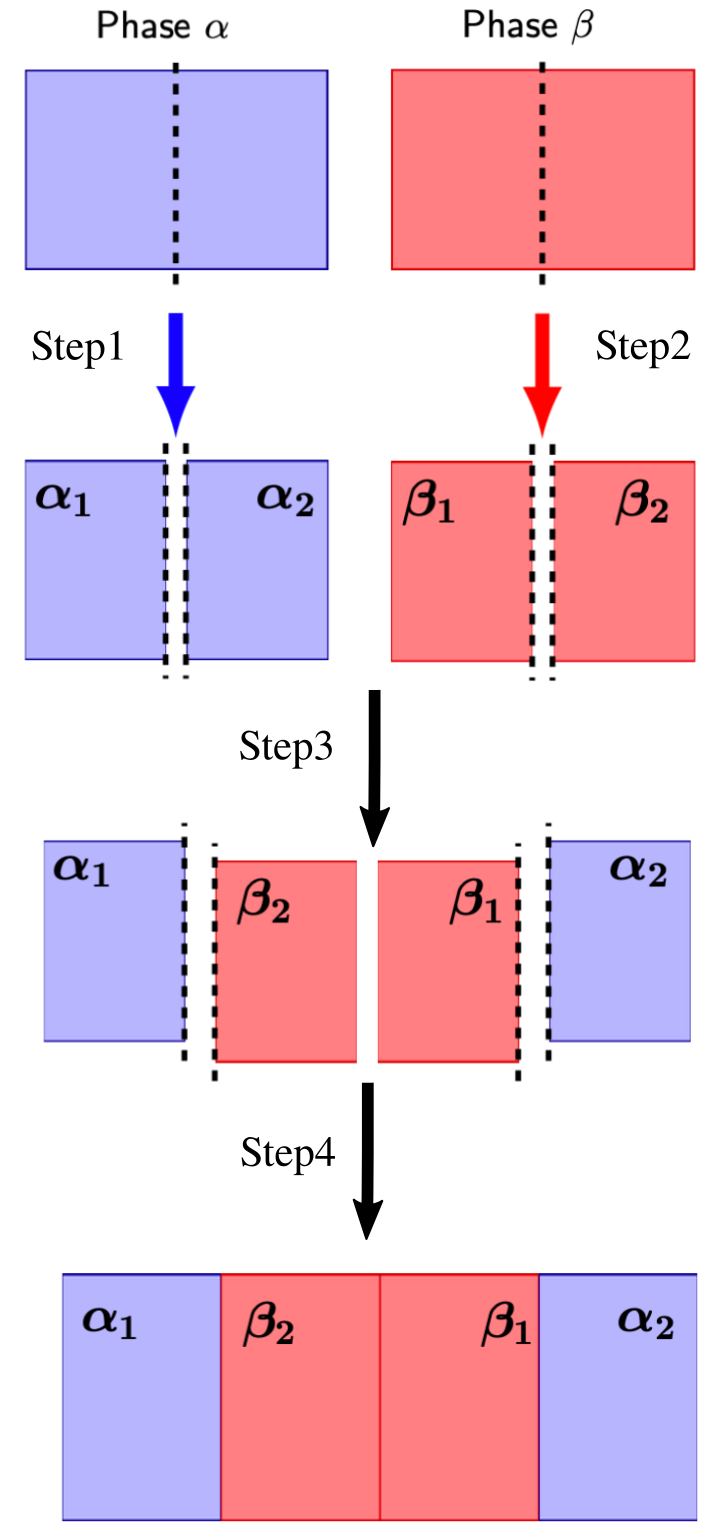
Direct determination of the IFE from the reversible work of creating an interface requires the careful design of a thermodynamic transformation path that starts from separate bulk phases equilibrated at coexistence conditions and ends with the same phases in contact across an interface. The cleaving method, originally proposed by Broughton and Gilmer 1 for the calculation of the solid-liquid IFE in a Lennard-Jones system, constructs such a path from four basic steps:
introduce an external ‘cleaving potential’ in the first phase (e.g. a solid);
same as 1., but for the second phase (e.g.) a liquid;
rearrange the boundary conditions to merge the systems while maintaining the cleaving potentials;
remove the cleaving potentials.
A sketch of a cleaving path to obtain the IFE between two generic phases \(\alpha\) and \(\beta\) can be represented as:
The reversible work in each step can be determined by different free energy computation methods, but those based on Thermodynamic Integration are the most straightfoward and provide accurate and direct results. With TI methods the free energy difference between two thermodynamic states connected by a transformation path is calculated by integrating the ensemble average of some configuration dependent function (e.g., the potential energy) with respect to a parameter defining the path from the initial to the final thermodynamic state.
To date, the cleaving method, which owes its name to the fact that each bulk phase is “cleaved”, i.e., cut at a certain position to create the new interface, has been used to calculate the solid-liquid IFE in hard and soft spheres 23, Lennard-Jones , TIP4P model water 45, Embedded-Atom Model (EAM) iron 6, silver-ethylene glycol , orcinol-chloroform and orcinol-nitromethane 7, as well as for the calculation of the surface free energy of molecular crystals, such as mannitol 8. However, due to the rather involved multi-step calculations required by the cleaving method, its use so far has been limited to a few research groups. Wider adoption of the cleaving approach for the calculation of solid-liquid and solid-solid IFE for different forcefields requires a more convenient simulation interface for the construction of the thermodynamic transformation path and calculation of the reversible work along this path. Here we attempt to fill this need with the CLEAVING package, which is designed to make it more straightforward for LAMMPS users to access the calculation of solid-liquid and solid-solid IFE in a wide variety of systems.
Table of Contents
Bibliography¶
- 1
J. Q. Broughton and G. H. Gilmer. Molecular dynamics investigation of the crystal–fluid interface. vi. excess surface free energies of crystal–liquid systems. The Journal of chemical physics, 84(10):5759–5768, 1986. doi:10.1063/1.449884.
- 2
R. L. Davidchack and B. B. Laird. Direct calculation of the hard-sphere crystal/melt interfacial free energy. Physical review letters, 85(22):4751, 2000. doi:10.1103/PhysRevLett.85.4751.
- 3
Ruslan L Davidchack and Brian B Laird. Crystal structure and interaction dependence of the crystal-melt interfacial free energy. Physical review letters, 94(8):086102, 2005. doi:10.1103/physrevlett.94.086102.
- 4
Richard Handel, Ruslan L Davidchack, Jamshed Anwar, and Andrey Brukhno. Direct calculation of solid-liquid interfacial free energy for molecular systems: tip4p ice-water interface. Physical review letters, 100(3):036104, 2008. doi:10.1103/physrevlett.100.036104.
- 5
Ruslan L Davidchack, Richard Handel, Jamshed Anwar, and Andrey V Brukhno. Ice ih–water interfacial free energy of simple water models with full electrostatic interactions. Journal of Chemical Theory and Computation, 8(7):2383–2390, 2012. doi:10.1021/ct300193e.
- 6
J Liu, RL Davidchack, and HB Dong. Molecular dynamics calculation of solid–liquid interfacial free energy and its anisotropy during iron solidification. Computational materials science, 74:92–100, 2013. doi:10.1016/j.commatsci.2013.03.018.
- 7
Ravi Kumar Reddy Addula and Sudeep N Punnathanam. Computation of solid–fluid interfacial free energy in molecular systems using thermodynamic integration. The Journal of Chemical Physics, 153(15):154504, 2020. doi:10.1063/5.0028653.
- 8
N. Di Pasquale and R. L. Davidchack. Cleaving method for molecular crystals and its application to calculation of the surface free energy of crystalline β-d-mannitol at room temperature. The Journal of Physical Chemistry A, 126(13):2134–2141, 2022. doi:10.1021/acs.jpca.2c00604.